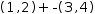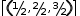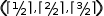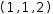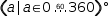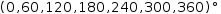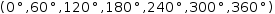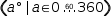3.7.3 Restructure
Restructure applies mathematically invalid structural transformations to collections and composites.
Contrast this with Distribute , which performs only valid transformations.
To illustrate, negation can be distributed across a tuple without changing its meaning.
That is, 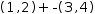 (1, 2)+-(3, 4) is the same as
(1, 2)+-(3, 4) is the same as  (1, 2)+(, -3, -4).
In contrast,
(1, 2)+(, -3, -4).
In contrast, 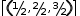 ⌈(1/2, 2/2, 3/2)⌉ finds the maximum value of a tuple,
but restructuring the ⌈...⌉ operator across elements of the tuple
transforms it to a tuple of ceiling operators
⌈(1/2, 2/2, 3/2)⌉ finds the maximum value of a tuple,
but restructuring the ⌈...⌉ operator across elements of the tuple
transforms it to a tuple of ceiling operators 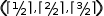 (, ⌈1/2⌉, ⌈2/2⌉, ⌈3/2⌉).
The latter tuple evaluates to
a completely different result,
(, ⌈1/2⌉, ⌈2/2⌉, ⌈3/2⌉).
The latter tuple evaluates to
a completely different result, 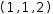 (1, 1, 2), because the transformation has changed the meaning of the operator.
(1, 1, 2), because the transformation has changed the meaning of the operator.
Structural transformations -- the kind where meaning changes -- are never performed by Distribute .
However, Restructure is still useful as a kind of shorthand for generating expressions. One might spread the degree operator
across elements of a tuple to see values of angles given in degrees converted to radians. The
tuple generator 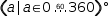 (a|a∈0, 360, 60) ° evaluates to
(a|a∈0, 360, 60) ° evaluates to 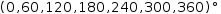 (0, 60, 120, 180, 240, 300, 360) °.
At this point, Distribute has no mathematical meaning, but Restructure happily applies the structural
change to produce
(0, 60, 120, 180, 240, 300, 360) °.
At this point, Distribute has no mathematical meaning, but Restructure happily applies the structural
change to produce 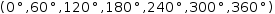 (, 0 °, 60 °, 120 °, 180 °, 240 °, 300 °, 360 °), which can then be evaluated.
Applied to the original tuple generator, Distribute again has no mathematical meaning, but Restructure transforms the generator to
(, 0 °, 60 °, 120 °, 180 °, 240 °, 300 °, 360 °), which can then be evaluated.
Applied to the original tuple generator, Distribute again has no mathematical meaning, but Restructure transforms the generator to 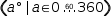 (a °|a∈0, 360, 60).
(a °|a∈0, 360, 60).